树的相关知识点(一)
一、 综述
树是一种在实际编程中经常遇到的数据结构,它是由n(n>=1)个有限结点组成的一个具有层次关系的集合,把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。树具有以下特点:
- 每个结点有零个或多个子结点
- 没有父结点的结点称为根结点
- 每一个非根结点有且只有一个父结点
- 除了根结点外,每个子结点可以分为多个不相交的子树
示例图: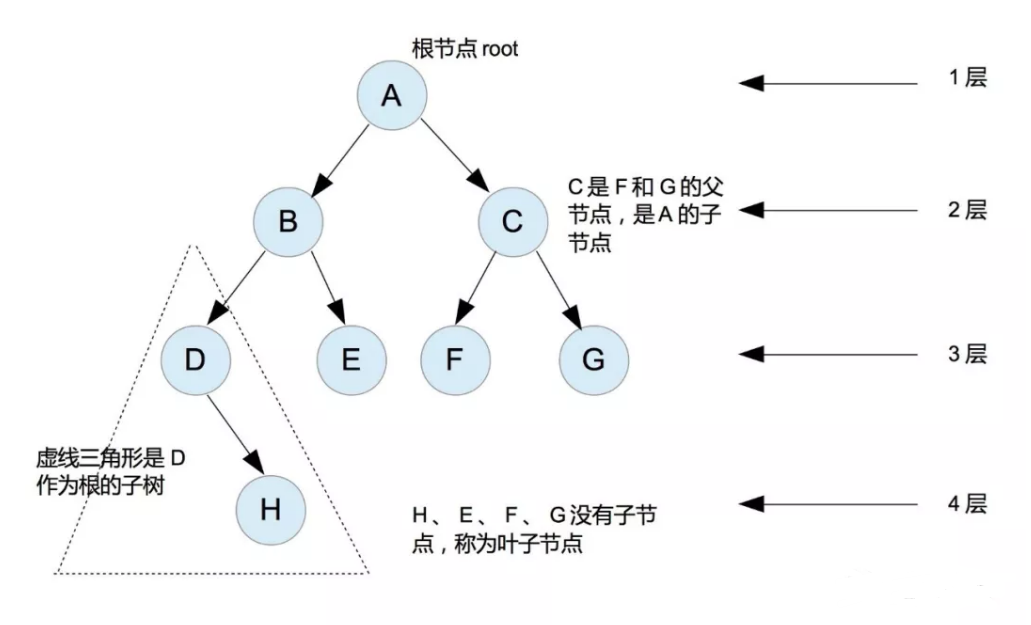
二、 相关名词
节点:上图的圆圈,比如A、B、C等都是表示节点。节点一般代表一些实体,在java面向对象编程中,节点一般代表对象。
边:连接节点的线称为边,边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。
路径:顺着节点的边从一个节点走到另一个节点,所经过的节点的顺序排列就称为“路径”。
根/根节点:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点,B是D的父节点。
子节点:一个节点含有的子树的根节点称为该节点的子节点,D是B的子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点,比如上图的D和E就互称为兄弟节点。
堂兄弟节点:父节点在同一层的节点互为堂兄弟
叶节点/叶子节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的H、E、F、G都是叶子节点。
子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推,D的层次为3。
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0,D的深度为2。
高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0,D的高度为1。
节点的度:一个节点含有的子树的个数称为该节点的度
树的度:一棵树中,最大的节点的度称为树的度
节点的祖先:从根节点到该节点所经分支上的所有节点
子孙:以某节点为根的子树中任一节点都称为该节点的子孙
森林:由m(m>=0)棵互不相交的树的集合称为森林
无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树。
有序树:树中任意节点的子结点之间有顺序关系,这种树称为有序树。
三、 二叉树的类型
二叉树:本身是有序树,且树的每个节点最多只能有两个子节点,即每个节点的度不超过2
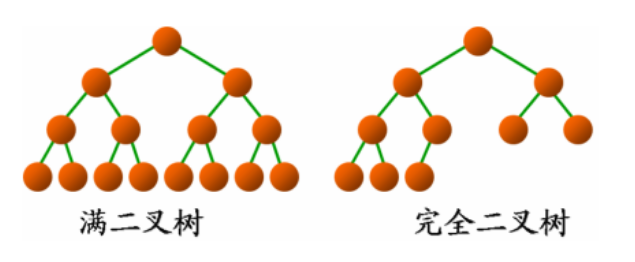
满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。也可以这样理解,除叶子结点外的所有结点均有两个子结点。节点数达到最大值,所有叶子结点必须在同一层上。
完全二叉树:完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。特点:叶子结点只可能在最大的两层出现。或者说,如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
注:完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
平衡二叉树之AVL树:平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
平衡二叉树之红黑树:红黑树是一种自平衡的二叉查找树
二叉查找树(BST)/二叉搜索树/二叉排序树:二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的节点。
带权二叉树:
- 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
- 结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
- 树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
哈夫曼树/霍夫曼树/最优二叉树:
- 给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
- 哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
四、 二叉树的性质
基本性质
- 二叉树中,第 n 层最多有 2^(n-1) 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2^(k-1) 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1
满二叉树的性质
- 满二叉树的深度为h,最大层数为k,深度与最大层数相同,k=h;
- 满二叉树第i层的结点数是:2^(i-1)
- 深度为k的满二叉树,总结点数是:2^(k)-1,叶子数为 2^(k-1),且总节点数一定是奇数。
- 二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 log2(n+1)。
完全二叉树的性质
- 完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
- ⌊log2n⌋ 表示取小于 log2n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2。
- 对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号,对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当
时,父亲结点为结点 [i/2] 。(i 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46+ 如果 ```2*i>n```(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 ```2*i``` 。
+ 如果 ```2*i+1>n``` ,则结点 i 肯定没有右孩子;否则右孩子是结点 ```2*i+1``` 。
# 五、 几个重要的二叉树 #
## 5.1 二叉查找树(BST) ##
### 5.1.1 定义 ###
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
+ 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
+ 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
+ 左、右子树也分别为二叉排序树;
+ 没有键值相等的节点。
### 5.1.2 性质 ###
二叉查找树的性质:对二叉查找树进行中序遍历,即可得到有序的数列。
### 5.1.3 复杂度 ###
+ 二叉查找树的时间复杂度:它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡(。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷。
+ 二叉查找树的高度决定了二叉查找树的查找效率。
### 5.1.4 基本操作 ###
二叉查找树的插入过程如下:
1. 若当前的二叉查找树为空,则插入的元素为根节点;
2. 若插入的元素值小于根节点值,则将元素插入到左子树中;
3. 若插入的元素值不小于根节点值,则将元素插入到右子树中。
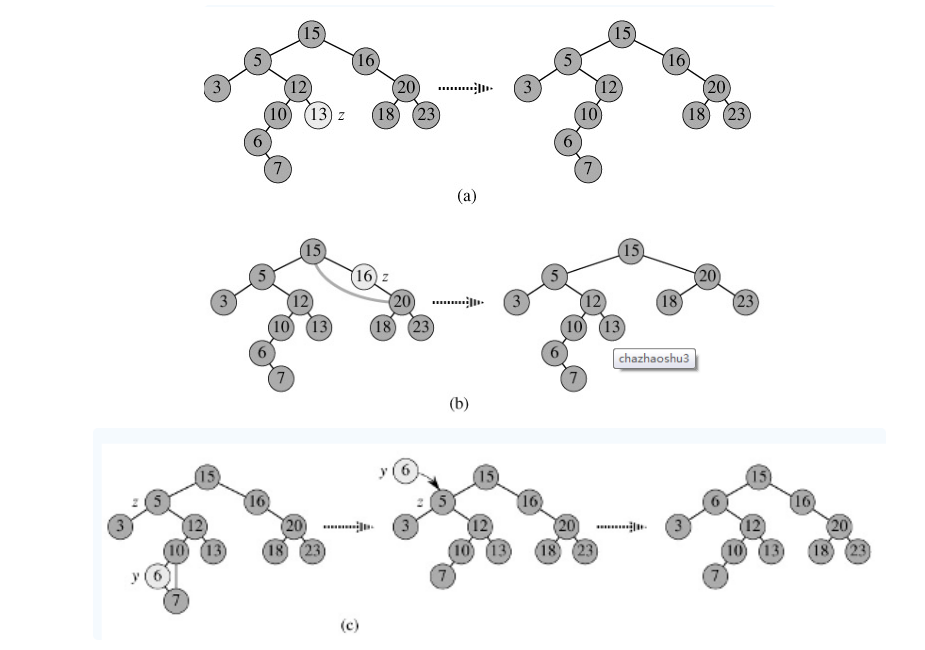
二叉查找树的删除,分三种情况进行处理:
+ p为叶子节点,直接删除该节点,再修改其父节点的指针(注意分是根节点和不是根节点),如图a;
+ p为单支节点(即只有左子树或右子树)。让p的子树与p的父亲节点相连,删除p即可(注意分是根节点和不是根节点),如图b;
+ p的左子树和右子树均不空。找到p的后继y,因为y一定没有左子树,所以可以删除y,并让y的父亲节点成为y的右子树的父亲节点,并用y的值代替p的值;或者方法二是找到p的前驱x,x一定没有右子树,所以可以删除x,并让x的父亲节点成为y的左子树的父亲节点。如图c。
## 5.2 平衡二叉树 ##
+ 我们知道,对于一般的二叉搜索树(Binary Search Tree),其期望高度(即为一棵平衡树时)为log2n,其各操作的时间复杂度O(log2n)同时也由此而决定。但是,在某些极端的情况下(如在插入的序列是有序的时),二叉搜索树将退化成近似链或链,此时,其操作的时间复杂度将退化成线性的,即O(n)。
+ 我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。
+ 于是就有了我们下边介绍的平衡二叉树。
平衡二叉树定义:平衡二叉树(Balanced Binary Tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用算法有红黑树、AVL树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log2n),大大降低了操作的时间复杂度。
最小二叉平衡树的节点的公式如下:
```java
F(n)=F(n-1)+F(n-2)+1
- 当
这个类似于一个递归的数列,可以参考Fibonacci数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。
5.3 平衡二叉树之AVL树
a)定义
AVL树又称为高度平衡的二叉搜索树。它能保持二叉树的高度平衡,尽量降低二叉树的高度,减少树的平均搜索长度,其定义如下:
- 本身首先是一棵二叉搜索树。
- 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
b)性质
- 左子树和右子树的高度之差的绝对值不超过1
- 树中的每个左子树和右子树都是AVL树
- 每个节点都有一个平衡因子(balance factor–bf),任一节点的平衡因子是-1,0,1。(每个节点的平衡因子等于右子树的高度减去左子树的高度 )
c)效率
- 查找、插入和删除在平均和最坏情况下都是O(logn)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
- 但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
d)AVL树的自平衡操作——旋转
- AVL树最关键的也是最难的一步操作就是旋转。旋转主要是为了实现AVL树在实施了插入和删除操作以后,树重新回到平衡的方法。下面我们重点研究一下AVL树的旋转。
- AVL树的基本操作是旋转,有四种旋转方式,分别为:左旋转,右旋转,左右旋转(先左后右),右左旋转(先右后左),实际上,这四种旋转操作两两对称,因而也可以说成两类旋转操作。
e)阅读资料
[1]数据结构之AVL树
[2]AVL树详解
[3][Data Structure] 数据结构中各种树
5.4 平衡二叉树之红黑树
a)定义
- 红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
- 它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的: 它可以在O(logn)时间内做查找,插入和删除,这里的n是树中元素的数目。
b)性质
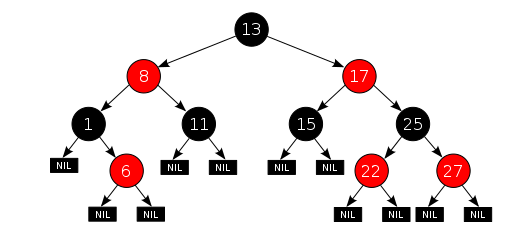
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制的一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
- 关键特性: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长
c)效率
它可以在O(logn)时间内做查找,插入和删除,这里的n是树中元素的数目。
d)红黑树的自平衡操作
- 颜色变更 + 树旋转
- 因为每一个红黑树也是一个特殊的二叉查找树,因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而,在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的性质需要少量(O(logn))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。虽然插入和删除很复杂,但操作时间仍可以保持为O(logn) 次。
e)阅读资料
[1][Data Structure] 数据结构中各种树
[2]Java 8系列之重新认识HashMap(HashMap引入红黑树优化)
其他树
B树
B树也是一种用于查找的平衡树,但是它不是二叉树。
B树的定义:B树(B-tree)是一种树状数据结构,能够用来存储排序后的数据。这种数据结构能够让查找数据、循序存取、插入数据及删除的动作,都在对数时间内完成。B树,概括来说是一个一般化的二叉查找树,可以拥有多于2个子节点。与自平衡二叉查找树不同,B-树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程,从而加快存取速度。这种数据结构常被应用在数据库和文件系统的实作上。
B+树
B+树是B树的变体,也是一种多路搜索树
B*树
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针,将结点的最低利用率从1/2提高到2/3。
Trie树
- Tire树称为字典树,又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。
- 典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
- 它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
参考资料
[1][Data Structure] 数据结构中各种树
[2]数据结构树(Tree)详解
[3]BST
[4]BST2
[5]手写二叉树-先序构造(泛型)-层序遍历(Java版)
[6]java:数据结构(四)二叉查找树以及树的三种遍历
[7]数据结构 《22》—- 二叉树三种遍历的迭代器算法
[8]树的四种遍历方法
[9]Binary Search Tree Iterator
[10]二叉树遍历(先序、中序、后序)
[11]浅谈数据结构-二叉树
[12]数据结构 - 树的种类及其应用
[13]二叉树的前序、中序、后序遍历迭代实现